Module: groundLocation

Executive Summary

This module allows the user to specify a single celestial-body fixed ground location \(L\). Reading in the planet’s ephemeris state the position of \(L\) relative to the planet origin and the inertial frame are evaluated at output as a message.

Further, one or more spacecraft states can be added to this module to compute the spacecraft position relative to the ground location \(L\). The associated output access output message contains the relative position vector in terms the spherical coordinates range, azimuth and elevation angle, as well as in terms of South-East-Zenith (SEZ) coordinates. Finally, the velocity of the spacecraft as seen by the \(L\) location is provided in terms of range, azimuth, elevation, south east and zenith rates. Finally, this access message has a integer variable indicating if the spacecraft is above a minimum elevation angle of the \(L\) SEC frame.

Module Assumptions and Limitations

This module assumes that the location is affixed to a spherical body with a constant radius. Elevation constraints are computed assuming a conical field of view around the normal vector from the body’s surface at the location.

Message Connection Descriptions

The following table lists all the module input and output messages. The module msg variable name is set by the user from python. The msg type contains a link to the message structure definition, while the description provides information on what this message is used for.

Module I/O Messages

Msg Variable Name	Msg Type	Description
planetInMsg	SpicePlanetStateMsgPayload	(optional) planet state input message. Default is a zero state for the planet.
scStateInMsgs	SCStatesMsgPayload	vector of sc state input messages. These are set through addSpacecraftToModel()
currentGroundStateOutMsg	GroundStateMsgPayload	ground location output message
accessOutMsgs	AccessMsgPayload	vector of ground location access messages

Detailed Module Description

The groundLocation module handles the following behavior:

1. Reads in the planet’s states using the planetInMsg input message

2. Conversion of latitude, longitude, altitude coordinates to planet-centered, planet-fixed coordinates

3. Conversion of relative position vector in SEZ range, azimuth, elevation, south, east and zenith coordinates

4. Determine the \(L\) relative spacecraft velocity as range, azimuth, elevation, south, east and zenith coordinate rates

5. Computation of spacecraft visibility (i.e. access) considering range and ground location field-of-view constraints

6. Support for multiple spacecraft given one groundLocation instance

Determining States

The position of the spacecraft in the SEZ frame, relative to the ground station, is parameterized by the cartesian coordinates:

(1)\[\mathbf{r}_{B/L} = x\hat{S} + y\hat{E} + z\hat{Z}\]

The cartesian coordinates are converted to spherical coordinates, centered at the ground station position, which give the range (\(\rho\)), azimuth(\(Az\)), and elevation(\(El\)).

(2)\[\rho = \sqrt{x^2 + y^2 + z^2}\]

(3)\[Az = \tan{\frac{y}{x}}\]

(4)\[El = \tan{\frac{z}{\sqrt{x^2+y^2}}}\]

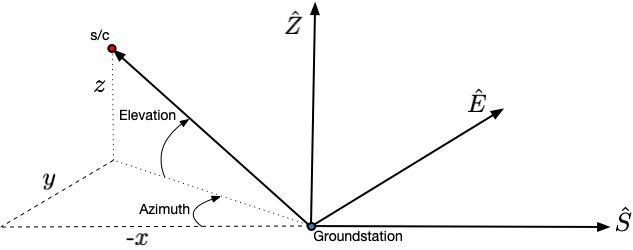
Figure 1: Diagram of the Azimuth and Elevation, in the South-East-Zenith frame

The spherical coordinate rates are computed by differentiating the range, azimuth, and elevation with respect to the rotating SEZ frame.

(5)\[\dot{\rho} = \frac{{}^L\text{d}}{\text{d}t} \rho = \frac{x\dot{x}+y\dot{y}+z\dot{z}}{\sqrt{x^2 + y^2 + z^2}}\]

(6)\[\dot{Az} = \frac{{}^L\text{d}}{\text{d}t} Az = \frac{1}{1+\frac{y^2}{x^2}} \bigg( \frac{y\dot{x}-x\dot{y}}{x^2} \bigg)\]

(7)\[\dot{El} = \frac{{}^L\text{d}}{\text{d}t} El = \frac{1}{1+\frac{z^2}{x^2+y^2}} \bigg( \frac{\dot{z}}{\sqrt{x^2+y^2}} - \frac{z(x\dot{x}+y\dot{y})}{(x^2+y^2)^{3/2}} \bigg)\]

User Guide

To use this module, instantiate the class and provide it with a body-fixed location (in either lat/long/altitude, via the specifyLocation method, or in planet-centered planet-fixed coordinates directly via the r_LP_P_Init attribute) and a planet position/attitude message (i.e., an instance of SpicePlanetStateMsgPayload); to compute access, at least one SCStatesMsgPayload message must be added to the module using the addSpacecraftToModel() method. The first spacecraft is 0, the second is 1, and so on.

A new instance of groundLocation, alongside necessary user-supplied parameters, can be created by calling:

groundTarget = groundLocation.GroundLocation()
groundTarget.ModelTag = "groundTarget"
groundTarget.planetRadius = orbitalMotion.REQ_EARTH * 1000.
groundTarget.maximumRange = 100e3 # Sets maximum range for visibility in meters
groundTarget.minimumElevation = np.radians(10.) #   Sets necessary minimum elevation for visibility to 10 deg in radians
groundTarget.specifyLocation(np.radians(0.), np.radians(0.), 0.) #  Sets location in latitude, longitude, altitude coordinates
scSim.AddModelToTask(simTaskName, groundTarget)

The planetRadius variable is optional and defaults to Earth’s radius. Instead of specifying the ground location through the specifyLocation() method, you can also set the module variable r_LP_P_Init using the specifyLocationPCPF() method. Avoid setting the module variable r_LP_P_Init directly, as there are computations that occur within the specifyLocation() and specifylocationPCPF() methods that are important for access message states.

The maximumRange variable is optional and defaults to -1. This means by default no maximum range is considered. Set it to a positive value to have hasAccess output message variable depend on range.

A groundLocation can be affixed to a specific planet by setting its planetInMsg input message:

groundTarget.planetInMsg.subscribeTo(planetMsg)

Spacecraft can be added to the model by calling:

groundTarget.addSpacecraftToModel(sc1.scStateOutMsg)
groundTarget.addSpacecraftToModel(sc2.scStateOutMsg)

#   log code
dataLog0 = groundTarget.currentGroundStateOutMsg.recorder()
dataLog1 = groundTarget.accessOutMsgs[0].recorder()
dataLog2 = groundTarget.accessOutMsgs[1].recorder()

---

class GroundLocation : public SysModel

#include <groundLocation.h>

ground location class

Public Functions

GroundLocation()

Creates an instance of the GroundLocation class with a minimum elevation of 10 degrees,.

Returns:

void

~GroundLocation()

Empty destructor method.

Returns:

void

void UpdateState(uint64_t CurrentSimNanos)

update module

Parameters:

CurrentSimNanos –

void Reset(uint64_t CurrentSimNanos)

Resets the internal position to the specified initial position.

bool ReadMessages()

Read module messages

void WriteMessages(uint64_t CurrentClock)

write module messages

void addSpacecraftToModel(Message<SCStatesMsgPayload> *tmpScMsg)

Adds a scState message name to the vector of names to be subscribed to. Also creates a corresponding access message output name.

void specifyLocation(double lat, double longitude, double alt)

Specifies the ground location from planet-centered latitude, longitude, altitude position.

Parameters:

• lat –

• longitude –

• alt –

Returns:

void specifyLocationPCPF(Eigen::Vector3d &r_LP_P_Loc)

Specifies the ground location from planet-centered, planet-fixed coordinates

Parameters:

r_LP_P_Loc –

Public Members

double planetRadius

[m] Planet radius in meters.

double minimumElevation

[rad] minimum elevation above the local horizon needed to see a spacecraft; defaults to 10 degrees equivalent.

double maximumRange

[m] (optional) Maximum slant range to compute access for; defaults to -1, which represents no maximum range.

ReadFunctor<SpicePlanetStateMsgPayload> planetInMsg

planet state input message

Message<GroundStateMsgPayload> currentGroundStateOutMsg

ground location output message

std::vector<Message<AccessMsgPayload>*> accessOutMsgs

vector of ground location access messages

std::vector<ReadFunctor<SCStatesMsgPayload>> scStateInMsgs

vector of sc state input messages

Eigen::Vector3d r_LP_P_Init

[m] Initial position of the location in planet-centric coordinates; can also be set using setGroundLocation.

BSKLogger bskLogger

&#8212; BSK Logging

Private Functions

void updateInertialPositions()

void computeAccess()

Private Members

std::vector<AccessMsgPayload> accessMsgBuffer

buffer of access output data

std::vector<SCStatesMsgPayload> scStatesBuffer

buffer of spacecraft states

SpicePlanetStateMsgPayload planetState

buffer of planet data

GroundStateMsgPayload currentGroundStateBuffer

buffer of ground station output data

Eigen::Matrix3d dcm_LP

Rotation matrix from planet-centered, planet-fixed frame P to site-local topographic (SEZ) frame L coordinates.

Eigen::Matrix3d dcm_PN

Rotation matrix from inertial frame N to planet-centered to planet-fixed frame P.

Eigen::Matrix3d dcm_PN_dot

Rotation matrix derivative from inertial frame N to planet-centered to planet-fixed frame P.

Eigen::Vector3d w_PN

[rad/s] Angular velocity of planet-fixed frame P relative to inertial frame N.

Eigen::Vector3d r_PN_N

[m] Planet position vector relative to inertial frame origin.

Eigen::Vector3d r_LP_P

[m] Ground Location position vector relative to to planet origin vector in planet frame coordinates.

Eigen::Vector3d r_LP_N

[m] Gound Location position vector relative to planet origin vector in inertial coordinates.

Eigen::Vector3d rhat_LP_N

[-] Surface normal vector from the target location in inertial coordinates.

Eigen::Vector3d r_LN_N

[m] Ground Location position vector relative to inertial frame origin in inertial coordinates.

Eigen::Vector3d r_North_N

[-] Inertial 3rd axis, defined internally as “North”.