Spacecraft Formation Flying

Spacecraft formation flying concepts have been studied since the beginning of the manned space program. The challenge at that time was to have two-spacecraft rendez-vous and dock onto each other. This was particularly crucial for the Apollo space program, which had the final lunar spacecraft being assembled in orbit. During this maneuver orbit corrections are performed not to correct the Earth relative orbit itself, but rather to adjust and control the relative orbit between two vehicles. For the docking maneuver, the relative distance is decreased to zero in a very slow and controlled manner.

The modern day focus of spacecraft formation flying has now extended to maintain a formation of various spacecraft. For example, the U.S. Air Force is studying concepts of having a cluster of identical satellites form a sparse aperture radar dish in space. Having multiple satellites flying at a specific geometry avoids the significant technical and financial challenge of attempting to build a radar dish of the equivalent size. These satellite formations can have diameters ranging from several dozens of meters to several kilometers. Attempting to build, control and navigate a light-weight radar dish structure that could span several kilometers would be very challenging and not cost effective. Instead, having a multitude of satellites form a virtual radar dish has the advantage of avoiding the structural flexing issues of the large dish structure and the associated pointing difficulties.

A conceptual difference between the formation flying problems that result in two or more vehicles docking and the spacecraft formation flying problem of maintaining the relative orbit of a cluster of satellites is that the later is significantly more sensitive to relative orbit modeling errors. If the satellites involved are being navigated to a rendezvous, then the formation flying period of the two vehicles is relatively limited compared to the lifetime of the vehicle itself. Typically, the rendezvous and docking maneuvers occur over 1-2 orbits. Thus, from a control perspective, if the relative orbit description contains some minor simplifying assumptions, then this will have a minimal impact on the control performance. The feedback control laws are robust enough to compensate for such modeling errors and will guide the spacecraft involved to a safe docking. Also, as the two vehicles approach each other, the relative distance becomes smaller and smaller. Thus any errors introduced into the relative motion description by making linearizing assumptions become negligible during the final docking phase.

However, for the task of maintaining a spacecraft relative orbit formation, where a cluster of satellites are supposed to continuously orbit each other, making linearizing assumption can potentially lead to a substantially higher fuel cost. The reason is that this formation is supposed to be maintained over the entire life span of the satellites. If a relative orbit is designed using a very simplified orbit model, then the formation station keeping control law will need to continuously compensate for these modeling errors and burn fuel. Depending on the severity of the modeling errors, this fuel consumption could drastically reduce the lifetime of the spacecraft formation. It is precisely this sensitivity to the orbital dynamics that makes this type of formation flying problem very interesting from the celestial mechanics point of view.

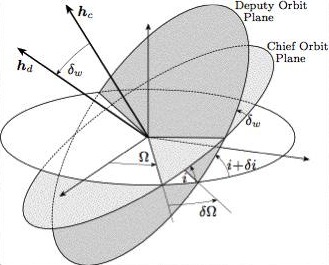The type of spacecraft formations typically considered in the current research consist of a cluster of satellites of equal type and built. Here each satellite ideally has the same ballistic coefficient. Thus, each orbit will decay nominally at the same rate. For this case it is possible to analytically find closed relative orbits. These relative orbits describe a fixed geometry as seen by the rotating spacecraft reference frame. Early research with colleagues at Texas A&M University has led to the development of J₂-invariant relative orbits. These relative orbit take advantage of the Earth's oblateness induced inertial orbit drifts and makes sure that all satellite will, on average, drift at equal rates. Further research has focused on developing various continuous and impulsive feedback control laws using both orbit elements and Cartesian coordinates. The use of the orbit elements has several advantages, since well established orbit perturbation theories can be exploited to only combat tracking errors that will cause secular drift. Further, the orbit element difference description of the relative orbits provides a convenient analytical solution to the general relative motion (for both circular and elliptic chief orbits) that is convenient for mission design or some control developments.